
□□

2021考研数学:浅析多元函数可微、连续与偏导数存在的关系
多元函数微分学是高数学习中的重要内容,是微积分学在多元函数中的具体体现,多元函数的可微、连续与偏导数存在之间的关系是学生在学习中易模糊的概念和难以把握的重要知识点。尽管它与一元函数的微分学有许多共同点,但它们之间也存在一些差异,这些差异是由“多元”这一特殊性引起的。由于多元函数的性质较为复杂,本文将针对二元函数的可微、连续与偏导数存在的关系进行探讨。在讨论三者关系之前,首先要对它们的概念进行充分的理解。这里的概念较为抽象,大家在学习中应该做到灵活理解,而非“死记硬背”式的学习概念。
在正确理解连续、偏导数及全微分概念的前提之下,我们根据考研大纲中规定的其相互关系进行如下简明阐述:
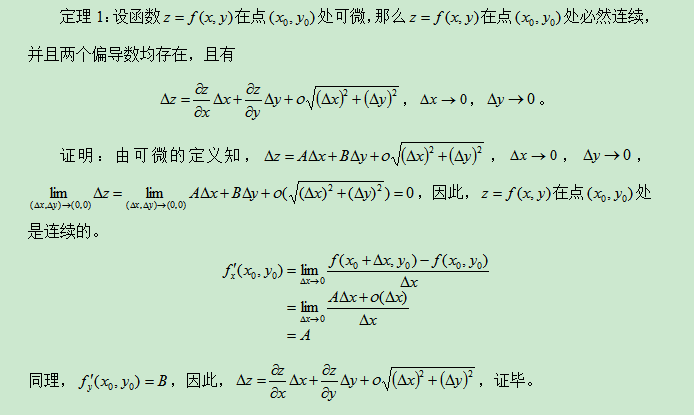


版权及免责声明
①凡本网注明"稿件来源:新东方"的所有图文、音视频等内容,版权均属新东方教育科技集团(含本网和新东方网)所有,未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。经授权使用时必须注明"稿件来源:新东方",违者本网将依法追究法律责任。
②本网未注明"稿件来源:新东方"的内容均为转载稿,本网转载仅基于信息传递之目的,并不表示认同其观点或证实其真实性。如拟从本网转载使用,必须保留本网注明的"稿件来源",并自负版权等法律责任。如擅自篡改为"稿件来源:新东方",本网将依法追究法律责任。
③如本网转载稿涉及版权等问题,请作者见稿后在两周内速与新东方网联系,邮箱:adm@xdf.cn。


