
考研数学冲刺复习,新东方网考研频道提醒考生注意把重点错题多看看。线性代数部分近几年出题比较稳定,结合真题,下面为大家预测三大考点,一起来梳理下,
线性代数近几年出题分析:客观题一般考查行列式的性质与计算、矩阵的性质与运算,解答题一般为求基础解系,求非齐次线性方程组的通解,求特征值与特征向量(定义法,特征多项式基础解系法),判断与求相似对角矩阵,用正交变换化实对称矩阵为对角矩阵(亦即用正交变换化二次型为标准形)。
一、线性方程组
1.判断含参数的线性方程组的解的情况并求解;
2.分析抽象类线性方程组的解;
3.公共解与同解问题;
4.线性方程组的应用;
5.矩阵方程求解。
【例题】2014年真题(适用数一、数二、数三)

二、相似对角化理论
1.求抽象类矩阵的特征值和特征向量,并进一步求出矩阵;
2.根据特征值和特征向量求矩阵中的参数;
3.矩阵相似对角化理论;
4.实对称矩阵的正交相似对角化理论;
【例题】2014年真题(适用数一、数二、数三)

【例题】2014年真题(适用数一、数二、数三)
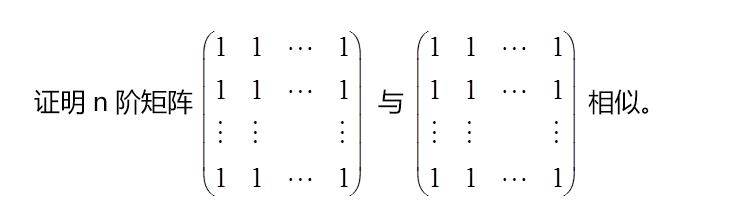
三、二次型
1.利用正交变换把二次型化为标准型的理论
2.正定矩阵与正定二次型理论
【例题】2013年真题(适用数一、数二、数三)



