2017考研初试12月24日至26日进行,新东方网考研频道时刻关注2017考研初试情况(点击查看》》2017考研初试真题及答案解析专题),并第一时间为考生提供考研真题答案及答案解析内容,同时新东方考研教师将为考生提供视频直播解析。敬请关注新东方网考研频道为您带来的精彩内容。教师解析专区|考研真题答案专区|考研历年真题
李良:各位考生大家好,今天2017的考研数学刚刚结束,我来给大家点评一下线性代数部分。
我们首先说今年考的两个大题,之前说过线性代数两个大题基本上围绕在解方程。纵观今年考题,线性代数部分重点知识考察比较突出。两个大题一如既往的考察了线性方程组问题和特征值、特征向量、二次型问题;小题分别涉及考察了判定矩阵可逆问题、判定矩阵相似问题、求矩阵的秩问题。
大部分题目的出题方式和以前考题出题方式类似,从整体来说还是强调要重视基础,重视历年考题。21题给了一个二次型,二次型里面还有一个未知参数A
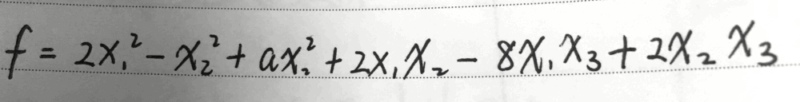
这跟2010年考的一个题很类似,把一个实对称矩阵通过正交矩阵把它变成对角阵,这个是通过把一个二次型正交变换变成一个标准型,这个叫反求问题。在我们以前考察当中实际上出现的次数还是比较多的。将一个二次型推过正交变换变成这样一个标准型,然后求这个A,求正交矩阵变换矩阵Q,这是比较常规的考法。
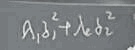
二次型一旦过正交变换,把它变成标准型,这个平方向系数其实就是它的特征值,从这种形式我们得到它的特征值有0,有两个特征值 l1、 l2,还有一个特征值是0。这个二次型矩阵的特征值有0,通过这个,我们可以把A给算出来。因为特征值有0,所以它对应矩阵行列式是等于0的,算出这个A。接下来求这个正交矩阵Q,把这个具体矩阵,求特征值求特征向量,将这个特征向量正交化、单位化,就完事,这是非常常规一种考法。所以这道题应该拿到11分,问题不是太大,在历年的真题里面专门去强调这个问题,应该是练的比较熟的。
接下来我们看一下第20题。今年计算量看,21题稍微去算一下,因为要算行列式、算特征值、算特征向量,你还得把它进行单位化、正交化,当然没具体算这俩特征值是什么? 20题其实计算量是比较小的,但是它涉及到一个证明问题。和 21题是重的,给了这么一个矩阵,A是一个三阶矩的,有三个不同特征值,然后给了α3等于α1加上2α,给了这么一个条件,然后呢让我们去证明r(A)=2,以及让我们再求一个抽象的方程。

这在今年最后的点题班里面,我专门提到过一件事情,因为这个抽象方程求解,太久没有涉及去考了,那么今年果不其然在这块我们涉及到的抽象方程让你进行求解的问题,我们也举过一个例子,第一问只要解决了第二问非常容易,关键这里面的质为证明质为R,这是证明的对象,如何去证明,这里面有三个不同的特征值。
这里涉及到特征值问题,如果是抽象矩阵涉及到特征值问题,你当然要从定义出发去处理它,所以这整个里面就只有这样一个条件,这个条件怎么去用,你把它用好了,这件事就搞定了。在抽象方程求解里面,这类问题咱是去写过的,这个东西处理起来跟咱讲那个题也差不多,你把它移过来是不是就
![]()
实际上这是
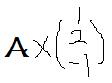
也就是得到这样一个齐次性方组,或者换句话说A乘它等于0乘这个东西,也就是说0是它的特征值。
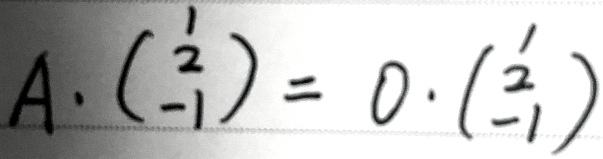
由于它有三个不同的特征值,说明0这个特征值一定是它的单根,由于三阶矩阵,有三个不同的特征值,它可以对角化的话,它是不是就跟那个对角矩阵是相似的,有一个特征值是0,还有两个特征值不是0,说明对角矩阵质数一定是R,A的质数也是R,所以第一问其实轻松就这么做完了,这实际上还是考了一个对角化问题。
第二个,让我们去求这个方程的非齐次通解,我们在说这种抽象方程进行求解的时候,非齐次通解是用齐次的通解加上一个非齐次的特解是不是就可以了。由于我们证明出A的质为R了,所以齐次的基础解无关个数只有一个,这个实际就可以作为基础的解析,所以K乘1、2、-1就叫齐次的通解,再加上一个非齐次的特解,非齐次特解有一个条件叫,这个非齐次方程是谁呢?这个非齐次方程叫做A,叫β等于α1+α2+α3,和以前考的题基本上是一样的,这个实际上反过来写一下是不是就是
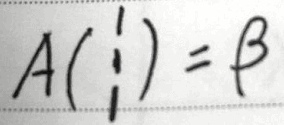
这个就叫非齐次一个特解,齐次的通解加上一个非齐次的特解,这道题就搞定,所以今年这个线性代数的这两个大题其实处理起来是比较容易的,至少从线代角度来说它是比较容易。
小题我拿到的也不是太全,有两个题,其中数学三的第五题判定可逆问题,这在教师带你做真题这个课程里面,我们在可逆问题判定上,实际上再往前应该是也不到10年是考过一个题。让你判定一个矩阵可不可逆作为一个小题,我们说判定可不可逆可以从几方面去处理:第一,如果有特征值的信息可以从它的特征值,只要证明0不是特征值,那么就是可逆问题;如果是具体的还可以从具体来算它的行列数。
这道题是给了这么一个条件,叫α是一个单位列向量,然后给了这么一个东西,让你判定
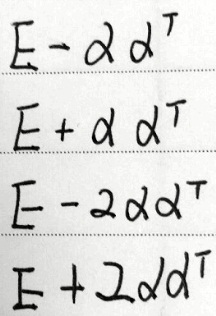
上面的这几个可不可逆。就是让你判定三种抽象矩阵可不可逆的问题。
主要从几方面可以入手,第一方面看能不能从定义,它能乘上一个矩阵等于单位矩阵就可逆了,第二个如果有特征值的信息,我们可以算它的特征值,如果特征值没有0,一定是可逆的,特征值有0一定是不可逆的。
还可以做什么呢,我们说如果是具体的还可以算行列值,还可以算它的质,像这道题的话,这里叫一列乘一行,这类问题在以前考的特别多的,一列乘一行,它的质一定是1,因为它是一个单位向量,一列乘一行它的质本身是小于等于1的,它是非0的单位向量,所以它的质一定为1。它的质一定为1的话,说明它一定是可以对角化的,说明它的特征值有0,0,0,0,0….N-1个0,然后呢接下来由于它是单位向量,它还有一个特征值就是它的解,还有一个是1。
实际上这道题就是从特征值这个角度入手,轻松就搞定,由于ααT所以这些特征值在这个基础上,像它加的1,它是在这个特征值2的基础上加1,你看看它有没有特征值为0,从这个角度我们判定可不可逆,所以这个4分也是比较容易。
所以线性代数今年考题相比较而言考的非常常规,跟以前考的很多东西都是类似的,把以前真题刷明白了,今年线性代数题其实还是很容易的。
还考了一个题是解决质问题,判定它的质。这个在以前我们总结质的时候,我们说有一些质的等式不等式关系。这道题其实考了它的等式关系,给了一个矩阵A,然后具体形式给你了,这里给了α1、α2、α3是无关的,叫列项量是无关的,叫列满秩的,然后就问你Aα1、Aα2、Aα3,这三个构成的质是多少,考一个质问题。
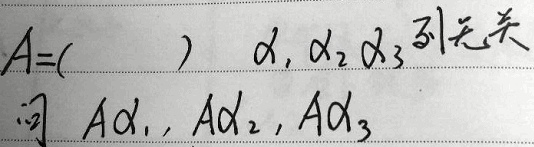
好,我们说只要考质问题的话我们常用质的等式不等式关系,用它质的等式关系的话,像这个我们说可以写成A乘以,把它分解一下,用分块矩阵乘法,这是不是叫A×B的质。这是A这是B,由于现在B叫什么列无关,并且它是三维向量的话,它就是一个可逆矩阵。所以A乘B的质,这一块都是可逆的,A乘B的质其实就是A的质,这是等式关系。所以A又是一个具体矩阵,你把它变换一下马上就能找到A的质,这就完事了。
还有一个题也是在近些年考的比较多的,又是判定相不相似的问题,是数学一的第六题,判定相不相似问题,这个我们当时给的判定方法,我们说具体的判定相不相似,相似问题。好了,这都是属于比较常考的题目,这个考了大家也不陌生,如果判定相不相似,是不是就看一下,如果特征值是一样的,均可对角化,那能判定出相似来。
这里的矩阵里边,像跟我在讲模拟题里边,这几个矩阵是很类似的,看相不相似,是不是可对角化的,然后特征值一样,均可对角化这就完事了,所以今年从整体而言线性代数考的东西是比较常规的,也就是说今年线性代数那30几分其实是比较容易拿到手的,而且计算量也不算太大,所以跟去年相比较而言,线性代数应该是简单的。
所以从刚才薛威老师也说过,今年整个平均分是比去年上升很多,因为去年平均分大概在60分左右,今年估计大概70,最少是在70以上。因为从线性代数角度,包括刚才薛威老师谈到高等数学部分,有一些题还是考的非常常规的,也有那么几个可能有点难度,因为出现有难度题目可能也是在高等数学部分。

【解析教师】李良
新东方在线教师,理学硕士,京城少壮派考研数学辅导专家。从事考研数学教学工作多年,对大纲和真题有深入研究。教学思路清晰,条理性强,分析准确到位。授课遵循深入浅出,循序渐进原则,有效做到使学生豁然开朗,在被数学折磨的绝望中寻找到希望。
【解析科目】2017考研数学线性代数真题及答案解析
【解析时间】12月25日11:30-13:30
考后关注》》
大学寒假进修指南》》
更多知识点请关注新东方网考研公众账号》》kaoyanxdf