微分方程是考研数学的一个必考点，并且还常常出两道题，占十几分，因此大家一定重视这一章，掌握好其基本知识和解题方法。微分方程中最重要的是线性微分方程，主要包括一阶和二阶线性微分方程，而线性微分方程又可分为线性齐次和非齐次线性微分方程，它们的解的线性组合是否仍为其方程的解?对这个问题，下面网校的蔡老师对它作些分析总结，供同学们复习参考。

　　一、线性微分方程的解的线性组合分析

　　下面对齐次和非齐次线性微分方程分别进行讨论。

　　1.齐次线性微分方程的解的线性组合性质

　　2.非齐次线性微分方程的解的线性组合性质

　　二、典型例题分析

　　注：此题是考研数学真题2010年数学二和数学三(2)。

　　从前面的分析总结可知，齐次线性微分方程的解的线性组合仍然是它的解，但非齐次线性微分方程的解的线性组合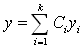，却不一定是它的解，只有当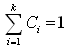时它才是其解，另外，当且仅当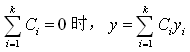

　　关键词：考研数学 线性微分方程 线性组合